Comprendre le SSL/TLS : Partie 2 Chiffrement

La cryptographie symétrique, également dite à clé secrète, est la plus ancienne forme de chiffrement. Elle permet à la fois de chiffrer et de déchiffrer des messages à l'aide d'un même mot clé.

Nous pouvons citer le chiffre de Jules César, qui consiste en un chiffrement par décalage.

C’est à dire que le texte chiffré s'obtient en remplaçant chaque lettre du texte clair original par une lettre à distance fixe, toujours du même côté, dans l'ordre de l'alphabet.

Chiffre de Jules César

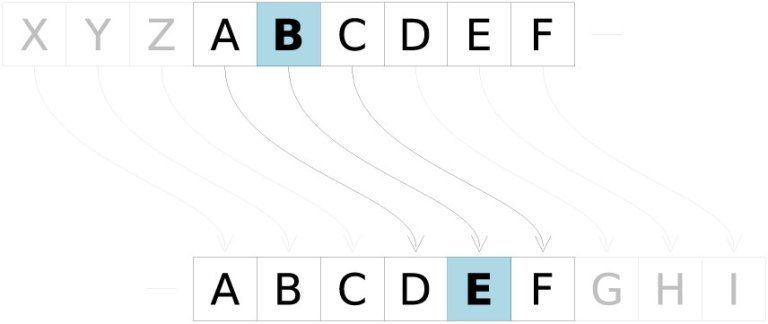
Bien évidemment, nous parlons ici d'un algorithme enfantin pour notre époque, mais si vous avez compris le principe qui s'applique ici, alors vous avez compris la cryptographie symétrique.

On retrouve, dans la catégorie des algorithmes symétriques, des monstres comme AES (ou encore DES, TripleDES, IDEA, Blowfish, CAST, GOST, RC4, >RC6…) qui est le plus utilisé et également le plus sûr aujourd'hui.

Ce dernier utilise des clés de 128, 192 et jusqu'à 256 bits soit un chiffre de longueur 1.157920892373162*10^77… (bon courage :) ). Si vous ne savez pas quel algorithme prendre, choisissez AES.

Pour décrypter un message sans connaître la clé, on peut utiliser plusieurs méthodes telles que :

• Essayer toutes les clés possibles avec son ordinateur, ou bien avec un ordinateur très puissant spécialement fabriqué pour casser un algorithme précis (ce qui a été fait pour le DES...).
• Se baser sur une faiblesse mathématique de l'algorithme et trouver des moyens de décoder le message ou trouver une partie de la clé.

L’avantage de ces types d’algorithmes est qu’ils sont rapides. Ce qui nous arrange lorsque nous traitons un grand nombre de requêtes HTTP.

Cependant, ces types d’algorithmes comportent un problème. En effet, il faut envoyer la clé grâce à laquelle nous avons chiffré le message à un destinataire.

Comment envoyer de manière sécurisée la clé au destinataire pour qu'il puisse déchiffrer votre message ?

Algorithmes asymétriques :

À la différence des algorithmes symétriques, les algorithmes asymétriques fonctionnent avec deux clés. On peut les appeler aussi, algorithmes à clé publique.

Les deux algorithmes asymétriques les plus connus sont :

• RSA (de ses concepteurs Rivest, Shamir et Adleman), qui est basé sur les nombres premiers.
• Diffie-Hellman

Le serveur crée deux clés (privée et public). Il envoie sa clé publique au client et garde bien secrètement sa clé privée.

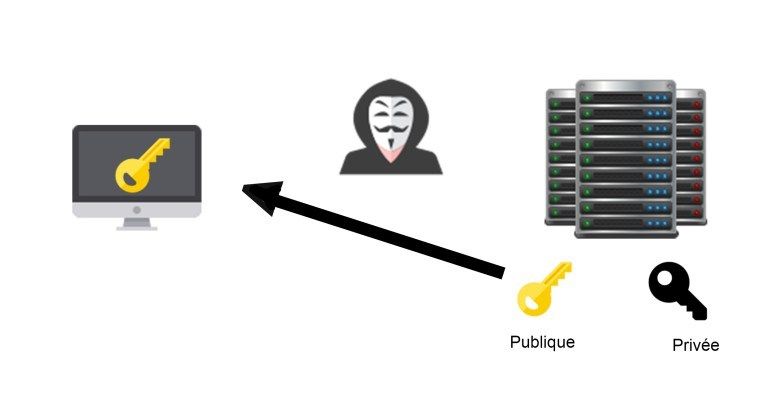
Si le serveur souhaite envoyer des données, il chiffre celles-ci via la clé privée. Le client pourra alors déchiffrer les données via la clé publique.

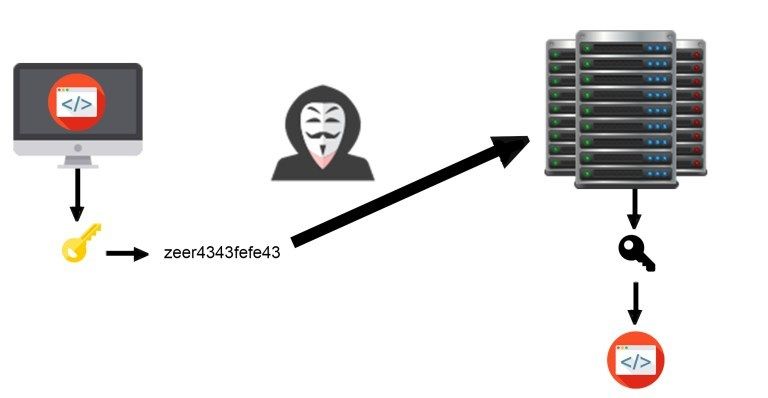
Inversement, pour envoyer des données au serveur, le client utilise la clé publique fournie par le serveur afin de chiffrer ses données. Le serveur utilise la clé privée afin de déchiffrer lesdites données.

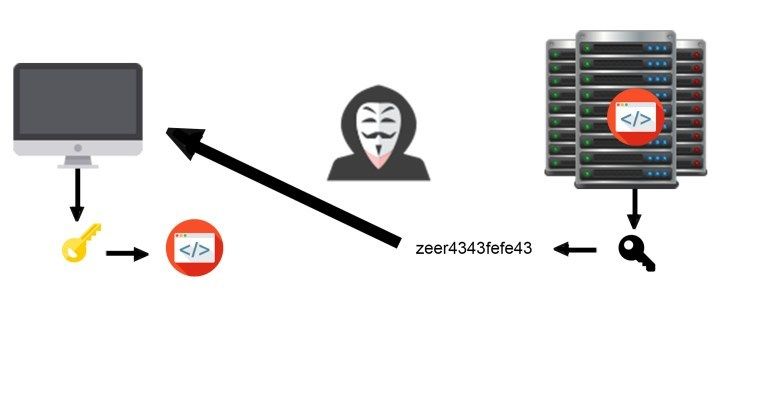
Le serveur est le seul à pouvoir déchiffrer les messages chiffrés par la clé publique grâce à la clé privé.

Si un hacker espionne votre réseau il aura "uniquement" accès à la clé publique et donc ne pourra pas déchiffrer les données.

Cependant, lorsque vous utilisez un algorithme comme le RSA qui effectue des opérations sur des nombres premiers, cela augmente énormément les temps de latences et consomme beaucoup de ressources. C'est pourquoi ces algorithmes sont uniquement utilisés pour l'échange des clés nécessaires à des techniques moins gourmandes.

De plus, la transmission de la clé publique pose un problème dans le cas où celle-ci n'est pas sécurisée c'est à dire qu'un attaquant peut se positionner entre l'entité et son public en diffusant de fausses clés publiques (par le biais d'un faux site web par exemple) puis intercepter toutes les communications, lui permettant d'usurper l'identité du diffuseur de clé publique et de créer une dite man in the middle.

Rassurez-vous les certificats peuvent résoudre ce problème grâce à la signature de tiers de confiance.